Notes about construction grammar

Bottom-up approaches to semantics like Montague semantics or recursive neural networks are usually considered fully compositional, in the sense that the meaning of a phrase, a clause or a sentence is mechanically computed from the meaning of individual words. But there are frequent and apparently non-compositional phenomena that throw off these semantic theories. And as a consequence of leaving aside semantics, one can also argue that top-down syntax either undergenerates or overgenerates.

Construction grammar is a radically different view of grammar. It can use a variety of features, not only syntactic, but also phonetic, discourse-related, semantic, pragmatic. It is conceptually simple, based on a single operation (unification), yet the underlying unification-based grammar formalism is more expressive than context-free grammars. Construction grammar is part of cognitive linguistics and as such, it tries to account for language acquisition and the use of mechanisms not specific to language, such as categorization. Construction grammarians also consider all data as equal, unlike generativists which distinguish between the core and the periphery in a rather ad hoc fashion. For all these reasons, construction grammar should appeal to cognitive scientists and AI researchers.

The first section motivates construction grammar for an audience mainly interested in the issue of compositional semantics, but it can be safely skipped. The second and main section is meant to be a partial summary of Fried and Östman (2004b)’s excellent introduction to Construction Grammar. All the pictures are taken from the article. I recommend the entire book from which it is taken (Fried and Östman 2004a). I found some explanations lacking in the article, in particular as to how unification works on the valence attributes, so there is a significant amount of guesswork here. Feedback is welcome!

Motivation

Compositional bottom-up approaches

Constructionist approaches to grammar assume that there are associations between meaning and expressions (substrings) of any size (word, phrase, clause, sentence). Such pairings are called constructions. This can be contrasted with projectionist approaches that assume that only words have arbitrary semantic representations, and that the representations of larger constituents are derived using bottom-up rules.

Let us briefly sketch how these bottom-up approaches work. Bottom-up approaches are guided by constituency trees. They include both formal, set-theoretic approaches like Montague semantics or connectionist approaches based on recursive neural networks. In such approaches, words have arbitrary meaning, but the meaning of constituents higher up in the constituency tree are completely determined by a bottom-up computation. Consider for example the sentence “John loves Mary”, which has the following tree structure:

        S            
    /       \        
  John      VP       
           /  \      
        loves Mary   

In Montague semantics, “loves” is associated with a meaning \(m_{\mathrm{loves}}\) that is a function, and “Mary” is associated with a particular individual (an element in a set) \(m_{\mathrm{Mary}}\). To obtain the meaning of the VP, we use function application, i.e. \(m_{\mathrm{VP}} = m_{\mathrm{loves}} (m_{\mathrm{Mary}})\). This resulting meaning \(m_{\mathrm{VP}}\) is another function, which takes an individual and returns a value that is either true or false, depending on our mathematical description of the state of affairs. In sum, the meaning of a parent is the application of the meaning of one of the two children on the meaning of the other children. For an introduction, you can read my notes on formal semantics until §“Content as intension” or Winter (2016)’s textbook on which they’re based.

In the bottom-up, connectionist semantics approach, such as Pollack (1990)’s recursive distributed representation, each word \(w\) is associated with a vector \(v_w \in \mathbb{R}^d\), and there is a composition function \(f: \mathbb{R}^d × \mathbb{R}^d \to \mathbb{R}^d\) that maps pairs of vectors of siblings to a new vector representing the parent constituent. In our example, the meaning of the constituent VP is \(v_{VP} = f (v_{\mathrm{loves}}, v_{\mathrm{Mary}})\).

Note that such approaches have not been abandonned. Formal approaches have fallen out of favor for various good reasons, but connectionist approaches have not. No, massive pretrained Transformers (Vaswani et al. 2017) used as encoders are not guided by syntactic trees. But there is still quite a lot of efforts towards unsupervised tree induction, i.e. learning to infer trees as hidden variables while optimizing for a particular objective (for example, see Maillard, Clark, and Yogatama (2019)’s work).

Examples of constructions in English

As different as these approaches are, they have an important common trait: they operate bottom-up. But it is frequent that we cannot trace some aspect of meaning of the sentence back to an individual constituent. This casts doubt on the bottom-up approach. To illustrate, let us look at the following usages of the verb “slice” from Goldberg (2006):

He sliced the bread. (transitive)

Pat sliced the carrots into the salad. (caused motion)

Pat sliced Chris a piece of pie. (ditransitive)

Emeril sliced and diced his way to stardom. (way construction)

Pat sliced the box open. (resultative)

First off, we see that “sliced” takes a variable number of arguments (2 in the transitive, 3 in the ditransitive). Moreover, the object closest to the verb in the ditransitive is not the same as the object of the transitive (Chris is not sliced!). Naively, it seems that “sliced” requires different lexical representations to handle these different contexts.

There are similarities of meaning between sentences which have different verbs, arguments and adjuncts but which share parts of their syntactic structure. For example, the two following sentences both have a “caused motion” interpretation (Goldberg 1995, chap. 17):

Pat sliced the carrots into the salad.

Fred stuffed the papers in the envelope.

The carrots and the papers move to the salad or the envelope as a (causal) consequence of the action of Pat and Fred. There are countless other similar examples with a similar interpretation, so loosely speaking, there seems to be a grammatical “pattern”.

Crucially, the “caused motion” interpretation is peculiar and unpredictable given the constituents of the sentence. It is not contributed by the verb because you can slice bread without the slices moving, as in the transitive use. It could come from the prepositional phrase, but if the “into” of the first sentence is clearly directional, “in” in the second is usually locative and can take different meanings. So even admitting that here, “in” is directional, we still need to explain why it is so. Thus we can rule out this explanation as well. Goldberg (1995, chap. 17) argues against other alternative explanations which state that the “caused motion” meaning is contributed by at least the verb or the preposition, but not always both.

Goldberg concludes that the grammatical pattern itself – a particular construction – contributes this meaning. We can make similar analyses for the other “sliced” sentences, and introduce other constructions which explain the particular interpretations of these sentences, interpretations that cannot be explained by the meaning of their constituents in isolation. If these sentences do not strike us as very idiomatic, it is probably because only a small “aspect” of meaning is contributed by the corresponding constructions.

But it is important to note that these constructions occur very frequently and are very productive, and therefore, we cannot simply treat them as exceptions. This will not happen in construction grammar, where constructions are first-class citizens. Construction grammar does not have the core/periphery distinction of generative linguistics, a distinction that looks (at least from outside) like a convenient fiction to ignore data.

I believe that in terms of expressivity, bottom-up theories of semantics can deal with such phenomena compositionally. That is, we can probably augment the representation of words (functions, vectors) so that they encode several possible argument structures at once. I think this is a consequence of extremely expressive representations and powerful composition operators (lambda-calculus is Turing complete and so are recurrent neural networks under some hypotheses). You can find more thoughts on that in the appendix. In that sense, I think that the argument given above is very limited. However, expressivity is not enough. In particular, we need a theory that accounts for language acquisition, and which explains how linguistic skills fits alongside with other cognitive skills. Although we won’t go into details here, construction grammar is part of cognitive linguistics and tries to answer these related questions at once.

From semantics to syntax

We’ve seen that constructions contribute meaning to an expression, which seems to be hard to handle bottom-up. This also threatens top-down, autonomous syntax (Chomsky 1957, sec. 8) as well. Goldberg (2006, chap. 2) argues against a derivational approach that would consider one construction as being syntactically derived from another. In the derivational view, from the syntactic structure of “Mina bought a book for Mel” we can derive the ditransitive form “Mina bought Mel a book”, independently of semantics. Goldberg shows that derivations both undergenerate (there are ditransitive which do not have a dative corresponding form) and overgenerate (vice versa). The root cause seems to be that constructions have different semantic constraints.

To deal with this, construction proponents generally claim that some semantics and pragmatics features should be in the grammar. It is not clear to me what should be considered part of grammar, as I can’t really tell apart some grammatical, nonsensical sentences from other ungrammatical sentences (in a principled, objective manner). But in my opinion, the elegance of construction grammar is more convincing than these arguments, so let’s leave aside theory and discuss construction grammar.

Construction grammar

In construction grammar (CxG), the grammar of a language is described as a set of constructions. Constructions themselves are formalised as attribute-value matrices (AVMs), also called feature structures. For programmers, it corresponds to the map/dictionary abstract data type, that is, it is a set of pairs of attributes and values.

The simplest kind of construction is the lexical construction. Every word is associated with a lexical construction. Here is a representation of the word “book”, taken from Fried and Östman (2004b):

The value associated to an attribute can be:

• Binary: here, the attribute lex is assigned the value +, indicating that the construction describes a single word, while lex - would be the value taken by a multi-word phrase.
• Categorical: the syntactic category attribute cat can take the value n (nouns), v (verbs), etc.
• An AVM: As illustrated here, nesting AVMs is useful to organize features into groups (syn, sem, but also phonological, etc.) and make reading easier. But as we will see later, it is also used to represent the hierarchical structure of constituents.
• An empty AVM: Represented as [], it is called variable (not illustrated here).
• A frame: A frame (book, here) is a structured representation of meaning, containing some entities with properties and that are related in some ways. I do not know the details of frame semantics and they are not necessary to understand this article.
• Values can be omitted for the sake of conciseness, which is indicated by [...] (not illustrated here).

Alternatively, we can specify a lexical construction using a different notation (Shieber 2003):

<lxm> = "book"
<syn head cat> = n
<syn head proper> = -
<syn level max> = -
<syn level lex> = +
<sem ...> = ...

and we call <...> paths.

Within a language, any set of attributes can be used. For instance, it makes sense to use a case attribute only for languages which have a case system (like Latin, but not English). Moreover, a given attribute is never required to be specified in every construction. For example, in English, many constructions do not specify any phonetic constraint, but some do.

Unification

How are these lexical constructions combined to form phrases and sentences? In particular, let’s see how we can form simple noun phrases. The English grammar allows noun phrases such as “the book”, “the snow”, “much snow”, but forbids the ungrammatical “much book”. This is an example of what is called an agreement relation between the determiner and the noun.

In construction grammar, the entire grammar is contained in the set of constructions. To form a phrase, phrase-structure constructions are used. They specify i) what combinations are allowed and ii) what features the result of the combination possess. As we will see, these phrase-structure constructions differ from lexical constructions, in that their AVM representations require special features.

Constructions are combined through a single binary operation called unification. Intuitively, this operation can be seen as a recursive union, fusion or merge of the AVMs. Crucially, this operation fails when two attributes exist in AVMs but differ in values. Unification verifies that the atomic attributes (binary, categorical) match if they exist in the two AVMs to unify; else the missing attributes are added from the other AVM. The unification procedure is called recursively on AVM values. Here is an example:

<x 3>
<y 4>
<z i 2>
<z j +>

<x 3>
<z i 2>
<z j +>
<z k ->

<x 3>
<y 4>
<z i 2>
<z j +>
<z k ->

Change the first line of the description of a or b by <x 2> and unification fails.

Let us try to model agreement between the determiner and the noun via unification. We partially specify the lexical constructions of “the”, “book”, “snow”, and “much”, focusing on the semantic features relevant for agreement: the configuration cnfg (whether it is a mass noun or a count noun) and the number num (singular or plural). We obtain something like:

• “much”: <sem cnfg> = mass, <sem num> = sg, ...,
• “the”: <sem cnfg> = [], <sem num> = [], ...,
• “snow”: <sem cnfg> = mass, <sem num> = sg, ...,
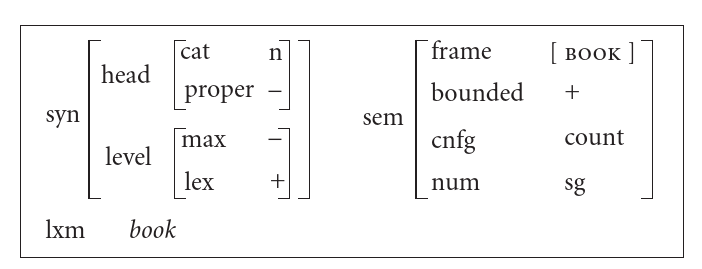
• “book”: <sem cnfg> = count, <sem num> = sg, ...,

In order to impose constraints on possible combinations of determiners and nouns, we want to create a phrase-structure construction that we would call the determination construction. If d1 and d2 are constructions corresponding to the words to combine, we would require that <d1 sem cnfg> = <d2 sem cnfg> (and similarly for the number attribute num). This is implemented using unification. We would like to state that the noun phrase is grammatical if and only if unification of d1 with d2 succeeds. If it succeeds, the words can combine and the resulting unified AVM can be used to determine how the noun phrase behave. In our example, the AVMs of “much” and “snow” can unify, since they are both labeled as cnfg mass. “The” combines with both “snow” and “book” because its cnfg feature is a variable: it is left unspecified and can unify with any value. However, this is not the case for “much” and “book”, which have incompatible cnfg feature.

The determination construction uses unification as outlined to ensure the agreement between its two children constituents. The agreement and other matching constraints make up the internal properties of the construction. In the determination construction of Fried and Östman (2004b), these internal properties are represented in the bottom boxes:

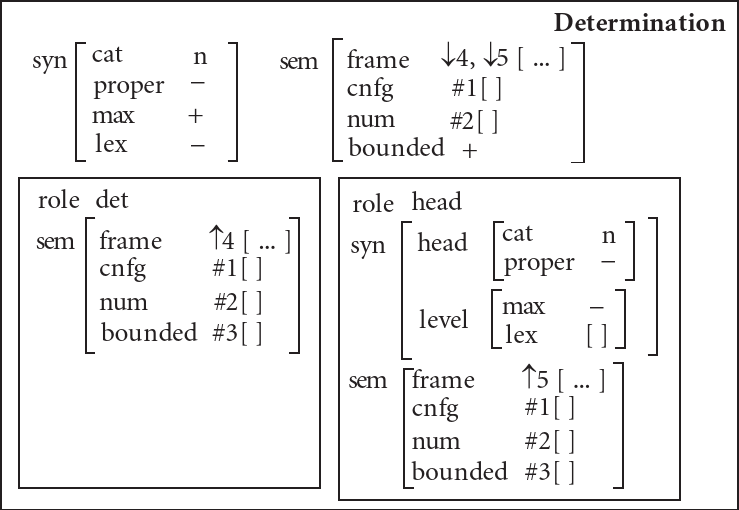
The internal properties are not associated with any attribute (they just float in the outermost box). So we see that this type of construction is not represented by a simple AVM like lexical constructions. Formally, this can be seen as an AVM with two special features (M. Kay 1984; Shieber 2003, p33):

• a constituent set, a set containing the daughters of the phrase,
• a pattern, a list specifying the order of realization of the daughter of the phrase (the actual order in which they are said).

For now, let us think of these boxes as defining the pattern, and the constituent set is just the set of elements in the pattern. One lexical construction can unify with the sibling on the left, and another with the one on the right.

Let’s examine the internal properties of the construction in more details. The #i syntax indicates coindexation, i.e. boxes prefixed with the same index \(i\) denote identical AVMs. In programming terms, two AVMs that are coindexed share a single location in memory. In this construction, coindexes represent the constraints that the semantic attributes cnfg, num and bounded must coincide in the two constituents. Besides these agreement constraints, we also see that one of the constituent is a determiner and the other is the head, and there are various syntactic constraints on the head. For instance, it cannot be a proper noun as we usually don’t say “the New York City”. Actually, in some cases this is possible, and this can be specified elegantly in the grammar (Fried and Östman 2004b).

By the way, coindexation is the reason for another representation of AVMs as directed acyclic graphs, where AVMs are nodes and attributes are edges. In this graphical representation, AVMs which share an index are a single node with several ingoing edges. This representation is important because it is used to implement unification (Jurafsky and Martin 2009, sec. 15.4), but we don’t need to discuss it further here.

If the constituent set contains the internal properties of the construction, what are the external properties of the construction? They are the features that are necessary to embed this construction, i.e. unify it with a larger phrase-structure construction as a constituent. Many internal features will be irrelevant to specify whether or not unification is possible. External features, on the other hand, should contain all the information about the phrase as a whole to specify with what it can combine, as a constituent of a larger whole. Some internal properties are resurfaced and passed upwards. Typically, the properties of the head are the most important – in particular, this is coherent with the traditional definition of the head word of a constituent as the word that defines the syntactic category of the constituent. Here, the cnfg and num values are the same as in the daughter constituents. Perhaps some verb’s (lexical) construction specifies that its object can only be a NP with a mass noun head, so these external properties might be useful. Moreover, we see that the bounded attribute is set to + regardless of whether the constituents are bounded or not. So not all external properties are simply internal properties passed upwards; some external properties are fixed.

Phrase-structure constructions can also be represented as i) a context-free rule and ii) equations (Shieber 2003). The equations either encode constraints on the daughter constituents (internal features) or specify external features. Here is the determination construction in this notation, where the syntactic features are omitted for conciseness:

X0 → X1 X2  # context-free rule
    # internal features (constraints on RHS)
    <X1 role> = det
    <X2 role> = head
    # internal features: matching constraints
    <X2 sem cnfg> = <X1 sem cnfg>  
    <X2 sem num> = <X1 sem num>
    <X2 sem bounded> = <X1 sem bounded>
    # external features (of LHS)
    <X0 sem cnfg> = <X1 sem cnfg>
    <X0 sem num> = <X1 sem num>
    <X0 sem bounded> = <X1 sem bounded>
    # end external features

In this case, the special feature specifying word order, pattern, is a list where X1 is the first element and X2 the second.

Linking constructions

We now come to the question of representation of verbs and linking. I think this is the really interesting and elegant part. A major question is how to account for alternations, that is, the fact that a single verb occurs in different syntactic context. This was the question that worried us in the motivation section. Consider the following alternations (P. Kay and Fillmore 1999):

1. Sidney gave some candy to Marion. (transitive, caused motion)
2. Sidney gave Marion some candy. (transitive, ditransitive)
3. Marion was given some candy (by Sidney). (passive, ditransitive)
4. Some candy was given to Marion (by Sidney). (passive, caused motion)

First of all, do we have to have four different lexical constructions to license these sentences? No, thanks to a mechanism called inheritance. We specify a general construction with which many, more specific AVMs will be unified. Here, we can have a single construction for “give” which doesn’t specify a lexeme (let’s call it the main construction), and then all the variants (“give”, “gives”, “given”, “gave”, etc.) inherit from the main construction while specifying a few additional attributes like lexeme, person, number, mood. Then, these more specific variants of constructions can unify with two constructions: either the transitive or the passive construction, and either the caused motion or the recipient constructions.

Inheritance is pervasive in CxG, because it allows linguists to express very general principles that hold in many “places” in the grammar without repetition. Most constructions, then, get their content by inheritance. This also allows more idiomatic constructions, which simply do not inherit certain widespread constructions. In English, there is a Subject construction from which all other verbs’ lexical constructions must inherit. This implements the requirement that all English sentences must have a subject.

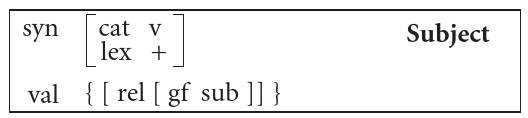
Let’s turn to lexical constructions for verbs and look at the Subject construction and the carry construction (Fried and Östman 2004b):

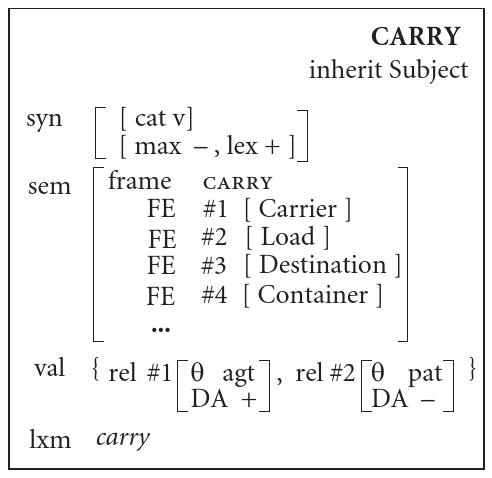
The carry construction introduces a valence (val) attribute. It is assigned a set of AVMs which each have a rel attribute. The function of val is to map some frame elements to θ-roles. This is the glue between the semantics and the syntax. Frame elements are entities fulfilling a certain role in the relation described by the verb. Here, the carry frame has 4 frame elements: Carrier, Load, Destination, Container. Similarly, the buy/sell frame would have 4 frame elements: Buyer, Seller, Goods and Money. θ-roles are generalizations of the frame elements. For example, both the Buyer of the verb “buy”, the Carrier of the verb “carry” and the Builder of the verb “build” are associated with the agent θ-role. Indeed, they share many properties: in general, they are volitionally involved in the action, aware of it, etc.

The valence only specifies particular salient frame elements which need to be expressed. For instance, in the carry construction above, the valence specifies that the Carrier and the Load are specified, which explains the common “She carried an oversized backpack” while forbidding “I carry”. Other frame elements are optionally expressed when the verb’s construction unifies with another construction that contributes valence. An example is given in the next subsection.

Here we need to take a detour and talk about how unification on sets work, in order to explain how verb constructions unify with constructions of their arguments. I haven’t figured out how it works exactly, so this should be taken with a large grain of salt. Please get in touch if you have any remarks. So here is my guess. In set unification, all the elements of the smallest set (or equal-sized set) try to unify with elements of the other set. If there is only one possible pairing, i.e. each element of the smallest set can unify with one and only one element of other set, we’re good and nothing special happens. But there are two other possibilities:

1. An element can unify with several elements from the other set. Then, it seems that we need to entertain several parallel options until unification with another construction resolves the ambiguity. In that sense, unification between 2 sets is not an operator (a function that yields a unique set) anymore.
2. An element cannot unify with any elements from the other set. Then, the element is added to the set (like a regular set union).

With this in mind, let’s go back to carry and Subject. The Subject construction asserts that one of the elements of the valence will play the grammatical function (gf) of subject. However, the inheritance of carry from Subject does not specify whether the 1st or the 2nd element of the valence is the subject (case 1). The ambiguity is resolved once carry unify with one of these two constructions:

• When carry is unified with Transitive Object, the non-distinguished argument (DA -) #2 is assigned the object (obj) function. This solves the ambiguity that we had with the inheritance from Subject: now, we know that the other argument #1, which does not have an attribute gf, must have the subject function.
• When carry is unified with Passive, the distinguished argument #1 is assigned the oblique function. It is only optionally realized, meaning that even if it is present in the linguistic analysis, it is invisible or omitted in the actual resulting phrase. This is indicated by (fni). When it is realized, it is a prepositional phrase with the preposition “by”. By inheritance from Subject, this implies that the argument #1, which does not have any function gf, must be the subject.

By the way, the DA attribute’s sole purpose seems to be to identify the argument that can be the subject in the active mood. It is a rather simple, but useful abstraction: we can still use the Passive construction and the subject is not the DA + anymore.

Increasing the valence

I mentioned above that constructions can increase valence. This will explain how the ditransitive construction can be applied to verbs like “slice” as we have seen in the motivation section. Fried and Östman (2004b) gives the following example of verbs usually considered intransitive that are used with a direct object:

She’ll walk you cross the street

Now we’re talking money!

It seems that to increase the valence of walk, we need to have a construction that specifies a valence element which cannot unify with any valence element of the walk construction (as I’ve hypothesized in bullet point 2). For example, consider the Affected Object construction:

It inherits from the Transitive Object construction. It adds i) a semantic constraint on the interpretation of the entire sentence and ii) specify the θ-role of the sole valence element. Since the single element of the two valence sets of Affected Object and Transitive Object are compatible, they unify (the semantics, omitted here, must match, too). However, since the construction of intransitive verbs like “walk” specify that the θ-role of their sole argument is not a patient, by bullet point 2, the valence set now contains 2 elements. This additional valence element licenses “you” in “She’ll walk you cross the street”.

Still, I’m not sure what prevents Transitive Object from unifying with walk directly. We would probably need two additional ingredients. First, an English-specific, grammar-wide rule that states that any valence element must specify a θ-role (see details in the details box below). Second, we would also probably need θ-roles to be mutually exclusive.

Ordering constructions

Lexical constructions, including verb constructions, do not have internal properties or daughter constituents. Neither do linking constructions like Passive or Transitive Object. That’s why they need to be unified with larger constructions such as the Verb Phrase construction.

We don’t need to go into details here, as we’ve seen all the important mechanisms of CxG. This construction has a verb constituent which appears first, followed by a variable number of arguments. These arguments are co-indexed with the valence specified by the verb’s construction. Co-indexation somehow prevents the subject element in the valence from appearing as an argument.

In fact, phrase-structure constructions are supposed to only define the hierarchy between constituents (via the constituent set). But in general, they do not need to specify how these constituents are linearly ordered in the sentence (via the pattern attribute); this is the job of ordering constructions. In English, phrase-structure constructions such as determination or Verb Phrase play both roles. On the other hand, in languages where word order is said to be more free, word order often carry discourse/pragmatic information. CxG is a good tool to describe this constraints, as AVM features can be of any nature. Fried and Östman (2004b) shows a Basic Clause Structure ordering construction for Hungarian which relies on discourse and phonological features. We can also read Lambrecht (2004)’s study of the “C’est X comme Y” construction in Spoken French for a detailed example.

At this point, we’re ready to define what a grammatical sentence is: it is a sentence which can be constructed as the result of the unification of a set of lexical, phrase-structure and ordering constructions. More precisely, the unification of the constructions specifies the order of its constituents via the pattern attribute, and these constituents themselves either possess a lexeme property or a pattern attribute specifying order of sub-constituents. The sentence is the recursive concatenation of these nested lexeme values.

Summary

• The grammar of a language is a set of constructions. There are several types of constructions.
• Lexical constructions only have external properties.
• Verb constructions are lexical constructions that are special because they have a valence set that specifies a minimal argument structure.
• Phrase-structure constructions specify a hierarchy via their constituent sets, but not necessarily their order.
• Ordering construction specify the order in which the constituent phrases appear (the pattern). In English, most/all phrase-structure constructions also specify an order but in other languages, the order can depend on discourse/pragmatics (“information structure”).
• Unification is an operation on constructions. It is relatively simple when we work with AVMs but messier when values can be sets.
• A sentence is grammatical iff there is a subset of constructions which can be unified, such that the pattern and lexeme values spell out the words of the sentence in the correct order.

Comparison with context-free grammars

Declarative vs procedural formalism

As we have seen, a phrase-structure construction or an ordering construction can be written as a context-free rule and some equations. This notation can be helpful to understand better how constructions differ from context-free rules alone. The equations specify two different things:

• constraints on the daughter constituents (internal properties, in the box representation)
• attributes of the constituent as a whole (external properties, in the box representation)

It might seem that this notation emphasizes the top-down generation process. Starting from the S non-terminal, the non-terminals are rewritten by replacing the LHS with the RHS of rules, until all the non-terminals have been replaced by a string of terminals.

But it should not obscure an important characteristic of unification-based grammars: the order of the application of the rules does not matter. Consider the sentence “John loves Mary” and its structure [NP [V NP]]. In context-free grammars, this is generated by applying the rule S → NP VP, then VP → V NP. But we cannot generate first V NP using the 2nd rule, then somehow identify this with the VP in the LHS of the first rule without parsing again. Nothing indicates that V NP is a constituent (a whole) that can be generated by a single non-terminal; In other words V and NP are not grouped in a single entity and do not carry external features. With construction grammar, and more generally, unification-based grammar, the information is not lost and we can generate in any direction:

• top-down: a VP construction unifies with V and NP constructions if the external properties of the V and NP match, as specified by the internal properties of the VP.
• bottom-up: a VP construction unifies with a S construction and a NP construction if the external properties of the VP and the NP match, as specified by the internal properties of the S.

We can create the final construction (that licenses a sentence) by applying rules in any order. This order-independence is what Shieber (2003) calls non-procedurality or declarativeness, but I don’t understand how it comes about exactly yet. For instance, Shieber (2003) warns us that various extensions of unification-based grammar threatens declarativeness, such as ANY values (that I’ve discussed in details boxes). However, I don’t see a way for ANY values to be present in the result of a unification with one order, but absent when we unify in another order.

No atomic non-terminals

Context-free grammars are also inelegant in that non-terminals are atomic symbols, i.e. they lack internal features. Take verb phrases, for example, and consider that verbs take a different number and different types of arguments (subcategorization). In CxG, the lexical construction specifies a minimal argument structure in a rather fine-grained way. Each such unique argument structure corresponds to a distinct verb phrase non-terminal in a context-free grammar. That’s a lot of non-terminals.

Since they’re atomic, these non-terminal do not encode any information about argument structure themselves. Only the rules tell us what they can generate.

Unification-based grammars are more powerful than context-free grammars

Shieber (1985) shows that natural languages are generally not context-free. He exhibits syntactic structures (cross-serial dependencies) from Swiss-German that cannot be produced by a context-free grammar. However, it is easy to imagine how these structures can be handled in the construction grammar framework. We can create a phrase-structure and ordering construction that would match the arguments and the verbs in the correct order.

Construction grammar (and unification-based grammars) are more powerful than context-free grammars. But I don’t know if unification-based grammars (without extensions like ANY) are equivalent to context-sensitive grammars, or some restricted subset of it.

Conclusion

I’ve tried to convince you that constructions are very frequent and pose challenges to bottom-up semantics. By seeing everything as a construction and using a simple mechanism to combine constructions, unification, one can describe complex linguistic phenomena elegantly and more or less formally. Moreover, constructionist approaches are appealing to cognitive scientists and AI researchers, because they try to account for language acquisition and place linguistic skills among more general cognitive skills.

In order to learn more about constructions, a fascinating follow-up read would be Lakoff (1987)’s “Women, fire, and dangerous things”. While Lakoff has pretty much the same definition of constructions as pairings of meaning and form, he goes much further in explaining why constructions are the way they are. In short, he argues that constructions can be in large part predicted (“motivated”) given i) a semantic description (“idealized cognitive models”) along with ii) general “central principles” that relate meaning and form within a language. In that sense, a construction is a “cognitively efficient way to express” meaning. Then, constructions are not (only?) related via inheritance in the space of constructions, but via metaphoric and metonymic mapping in semantic space. I would like to summarize that in the future.

I also hope to read and perhaps comment Goldberg (2006)’s second book, which deals with learning and generalization.

Appendix

Bottom-up semantics and constructions

How can we reconcile bottom-up computation of meaning and seemingly non-compositional phenomena that are explained via constructions?

Let us start with formal semantics. If we do not modify the composition operator (function composition), in order to change the semantics of phrases of multiple words, we have to change the meaning of individual words. We could associate each verb with several meaning functions, each taking a different number of arguments, and each of these arguments could also have different syntactic types (noun phrase, prepositional phrase, adjective phrase).

The different senses of the verbs in different constructions are still very close to each other, and naively duplicating the meaning functions and only “changing some minor aspect” in the resulting function would not capture these similarities. Instead, we could create a function that derives the specific meaning function from a basic (say, the “transitive”) meaning function. This would be in-line with the general spirit of formal semantics, heavily relying on lambda-calculus. For example, one could imagine a function \(f_{\mathrm{caused-motion}}\) and apply it to the generic meaning \(m_{\mathrm{sliced}}\) to derive the “caused-motion meaning of the verb sliced”.

Still, this would be a constructionist solution, in that specific constructions would get dedicated representations as functions. It would also be projectionist, in that meaning is completely encoded in the lexicon. I guess this is one way in which, as Levin notes, both approaches converge.

There are still important problems.

1. Since there are several possible constructions per verb, to analyze a given sentence, how do we choose which function should be applied? We could start different semantic analysis of the sentence in parallel (bottom-up) by applying the different functions. As soon as there is a mismatch in the number of arguments or the syntactic category of the arguments, a given interpretation stops being considered and is pruned. But note that this would not be enough to distinguish the “way construction” from the “caused motion”, which both have an additional NP argument compared to the “transitive”.
2. Constructions such as the “caused motion” are very productive. It seems that we can’t really list all the verbs that can be used in this sense.
3. There are constructions that lack verbs (Goldberg cites examples from French, Russian, German).
4. It is probably not great to consider that the transitive construction is neutral. Indeed, we can use intransitive verbs such as “walk” within the transitive construction, so it cannot really be neutral.

Let us directly turn to the connectionist approaches. We can naively assume that the vector of a given verb encodes whether or not the verb can enter the construction. Then, the composition operator \(f\) could vary slightly its outputs to incorporate the additional meanings contributed by the constructions. Does the connectionist approach suffer from the problems above?

Point 2) indicates that whether a verb can enter a construction or not must be a matter of generalisation, since we don’t see all the possible verb/construction pairs during language acquisition. Then we hope that whether a verb can enter a certain construction is computed by a certain function of syntactic and semantic features. (This probably also solves 1) at once.)

Again, this is in some way a constructionist solution: for each construction, we can try to find within our neural network \(f\) (via some sort of probing, for example) a subnetwork that predicts, for any verb vector, whether this vector potentially participate in a certain construction. This relies on the existence of constructions.

References